Ready to streamline? Discover how BlendOpt enhances planning and scheduling
The simultaneous optimisation of processing strategies, stockpiling, and product strategies within BlendOpt
Introduction
To remain competitive and respond quickly to changes in market conditions miners will need to develop a holistic strategy for value creation as well as improve the coordination of operations planning across the mining value-chain.
Plans for mining, processing, logistics, and marketing are difficult to align with enterprise objectives if each planning activity is developed separately instead of holistically. In practice, value-chain optimisation is only achievable through integrated planning. By integrated planning, we mean coordinated planning of decisions between mining, processing, logistics, and sales. While the importance of integrated planning is recognised, its execution is difficult without the right tools to support this process.
BlendOpt is the first mathematical optimisation software tool that supports complete integrated planning of sales and value-chain strategies. Starting with a mine schedule, BlendOpt discovers strategies for how product should be processed, blended, and allocated to different products or sales contracts with the objective of maximising profit. Mathematically optimised plans are created using algorithms that test billions of possible plans in search of the highest profit from the data provided.
Previous mine value-chain optimisation software has historically been unable to accurately model the problem and did not contain algorithmic techniques that could solve the problem in a timely fashion or address the multitude of mining value-chain constraints. In addition, any results generated were difficult to analyse thereby limiting what insights could be gained to inform practical improvements to business strategy, or tactical and operational decision making.
In this article we will be exploring these themes and help you to understand how BlendOpt can unlock additional value within your operation.
Defining the right problem
Solving the right integrated planning problem can influence whether operational decisions will align across a mining value-chain - in this article we will explore how changes to the fidelity of sale price models and cost models can significantly alter the financial optimality of processing and marketing decisions. This type of interaction between business silos is very common and presents significant challenges to miners who would like to unlock additional value from their operation.
Challenge current planning assumptions
Challenging long-held planning assumptions and posing alternatives can sometimes act as a catalyst for realigning decisions across a value-chain. In this article we'll be comparing existing intuition-based wash-bypass decisions at two Australian operations with mathematically optimised decisions derived by BlendOpt.
Integrated operations - a new priority for the mining industry
Market conditions will no longer allow for operations that are not competitive in costs and cash flow. While asset quality is paramount, competitiveness is also influenced by operational decisions made across a value-chain.
The effectiveness of operational decisions is limited by their coordination and subsequent alignment. In other words, what is a good decision for each separate business unit depends on those decisions made within other units. Silo business drivers for mining (ROM tonnes), processing (utilisation), and marketing (revenue) only align with enterprise objectives (cash flow, NPV) when operational performance is low. Under high performance operating conditions, decisions guided by silo KPIs will misalign with the interests of the group and erode value (March, 1991; Levinthal and March, 1993).
This is particularly true of many mining processing decisions and their interdependency with decisions in mine planning, logistics, and market planning. Decisions in processing impact product quality, product specifications that can be achieved and thus sold, production yields and operating costs.
In practice, value-chain alignment requires the coordinated planning of decisions between mining, processing, logistics, and sales. While the importance of integrated planning is recognised, its execution can be challenging. Understated difficulties arise in data integration and technical challenges arise in the creation and optimisation of an integrated plan (King, 2004; Whittle, 2010). Also important are the organisational challenges to realising effective coordination at every stage of the planning process from agreement on scope, procedures for plan development, plan refinement and execution.
While such challenges can be less important in a high margin operating environment, many miners face a convergence of challenging conditions that increase the importance of integrated planning. In particular, integrated planning becomes more significant as easy access high-quality single seam operations are replaced by more complex multi-seam operations and also as price compression across some mined products creates new questions about how a producer should process, blend and market their product.
Integrated Plan Modelling Requirements
When undertaking a planning exercise, it's important to model only those constraints and problem features that significantly influence the calculated performance of a plan. When relevant problem features are ignored, the performance of decision options will not be accurately evaluated and can become misaligned with the actual financial metrics of an organisation. For instance, ignoring the difference in operating costs between wash and bypass can bias mathematical optimisation in favour of higher quality products. In this section of the article, we will discuss this and other relevant considerations when solving the integrated coal planning problem.
Product price models - using coal as an example
In a coal context, product targets for Ash, Calorific Value, CSN, Volatile Matter, Total Sulphur and other quality attributes can be important constraints in an integrated planning exercise. Defining these quality requirements as a range as well as a target value is sometimes helpful to ensure the optimisation of product quality is constrained within acceptable bounds.
Production plans sometimes must deliver contracted volumes by specified dates in addition to maximising profits from non-contracted sales. For some operations, defining a maximum product volume can be used to reflect sales expectations for each product and thereby introduce practical constraints into a mathematically optimised planning process.
In practice, a product's sale price can change due to several factors including market and currency volatility. For high volume producers, the total tonnage sold may also influence sale price due to customer requirements for volume based discounts or due to the impact of volumes on regional or global supply. The delivered product quality can also alter the final sale price as specified within contractual agreements.

Within a coal value-chain, some quality attributes such as Hargrove Grindability Index, Vitrinite reflectance, and Crucible Swelling Number display non-linear mixing relationships such that it is not possible to accurately predict blended coal quality using a weighted average of the individual components (Van Niekerk and Dippenaar, 1991; Vasko et al, 2005). Without an accurate model to predict blended qualities, it may be necessary to introduce additional blending constraints. For instance, constraints may be needed to prevent materials from being added to a product based on pre-blended quality characteristics, constraints may require explicit rules that include/exclude particular seams/plys from a product, or constraints might require products to consist of at least or at most a designated percentage of a seam by weight. The relationship between coal properties and coking properties also exhibits a non-linear relationship that may similarly require additional blending constraints.
CHPP Modelling Requirements
If the CHPP is at risk of becoming a value-chain bottleneck, then modelling maximum operating capacity will ensure planned product coal volumes are achievable. Operating capacity may need to be modelled to change over time to reflect planned maintenance or other expected events. In some circumstances the CHPP feed rate will depend on the seam processed and there are circumstances where feed blending can positively or negatively impact feed rates, which influences operating capacity and may also need to be modelled.
If there are options to wash or bypass coal, then it is typically beneficial for these decisions to be mathematically optimised as they substantially impact operating costs, production yields and final coal quality. The relevance of mathematically optimising CHPP operating parameters depends on coal washability and infrastructure. If CHPP operating choices are straightforward due to particle density distributions or the curvature of the ash:yield relationship, then it might only be necessary to optimise wash versus bypass decisions. In many circumstances however there will exist dense medium cyclones (DMC) for coarse coal with cut-points that should be mathematically optimised, assuming availability of accurate data. While the impact of DMC density on quality and yield can be quantified, rules and logic will sometimes provide insufficient guidance on how wash decisions impact final product blending options, contracted sales obligations, product pricing and total revenue. This is particularly the case for complex deposits containing many seams or ply groupings.
In some CHPP designs, DMC rejects can be fed to a secondary DMC circuit, with the decision to operate the secondary circuit depending upon reject material properties. In this case there is typically the option to allocate processed coal from the secondary and primary DMC to different products. The CHPP design sometimes allows other processed size fractions to be allocated to either primary or secondary products, and these decisions can also be optimised for some operations.
For short-term planning exercises, realistic CHPP processing plans may also need to account for other practical considerations such as minimum campaign size and stockpile rehandle costs.
Stockpile Models
If short-term plans are being generated with daily or weekly time intervals, it could be important to model stockpiles due to their impact on blending options and ship loading. With shorter term plans there may also be an option as to whether coal should be stockpiled or directly fed to the CHPP which may also need to be optimised. Stockpiling is relevant to the integrated planning problem because it introduces a rehandle cost and influences material qualities as a result of the blending of material onto the stockpile. In some cases rehandling coal influences particle size distributions and coal liberation with a corresponding influence on yield and clean coal quality attributes.
The need to model stockpiles at different locations in the value-chain will depend on context and may require models for ROM stocks, processed coal stocks, and port stocks. Initial inventory levels may need to be modelled due to their direct influence on a plan's physical accuracy.
Minimum and maximum stockpile capacities can also be important model constraints. Allowing modelled stockpile capacities to change over time can enable a plan to account for scenarios involving forced stock depletion as well as enable the build-up of stock e.g. for a rainy season.
If there is any likelihood of coking coals remaining on a stockpile for a significant period of time then it may become necessary to model changes to coal quality that take place as a result of oxidative 'aging' eg loss of fluidity. In these circumstances, it may also be necessary to include constraints on the maximum time that coal is permitted to remain on a stockpile before it is reclaimed.
Blending models for stockpiles can also be important to the realism of a plan. Common models include weight averaging, first-in-first-out, and last-in-first-out models as well as combinations of the above. Assuming the availability of data, more complex bench models or 3D models might also be useful for short-term scheduling.
Value Chain Modelling
If coal is sourced from different geographic locations using different assets, it may be necessary for capacity constraints to be defined for the transport of ROM from different locations. Similarly, there can be constraints on what coal can be processed in each plant including options for coal to be processed at one of multiple plants. Time-based rail and port material flow constraints may also be considered if these have the potential to act as bottlenecks within the value chain.
Coal sales to domestic buyers are unlikely to have the same downstream costs as exported coal. These cost model differences may need to be considered as it can influence product ratios and blended product quality decisions. Conversely, some operations purchase domestic 3rd party coal that is blended with internal production prior to sale in the export market. Third party coal purchases will have their own contractual obligations, costs and price structures that may need to be accounted for to obtain accurate financial comparisons of planning alternatives.
Other Relevant Issues
One of the most significant challenges integrated planning arises from the need for optimisation across a planning horizon. For instance, plans that must achieve future contractual requirements may require an ability to measure how decisions in one time period will affect the decision options available in a later time period. Most mining software that implements mathematical optimisation techniques has been designed to solve each time period in isolation of all others. This may cause challenges in satisfying contracted sales if the optimal plan requires strategically holding coal to meet future contract requirements or more generally to deliver the maximum profits from an operation. Similar difficulties can arise when planning CHPP processing decisions. For instance, there is sometimes a need to process or not process certain stocks to prevent a future CHPP bottleneck.
The importance of strategic "look ahead" optimisation influences which optimisation algorithms are suitable for solving this class of problems. Other problem aspects that influence algorithm suitability include stockpile modelling requirements, non-additive blending relationships, and price function modelling.
Time granularity is also an underappreciated complexity within the integrated planning problem. Although there is uncertainty in the exact timing of future mining activities, it is important for plans to be defined at short time intervals (eg weekly) to impose a conservative constraint on the materials that will be available to blend together at a single point in time. For this and other reasons, the size of integrated planning problems can be very large. BlendOpt has been applied to problems with dozens of plys actively mined at a single time from multiple pits along with multiple processing, stockpiling, and product decision options. Considering such a problem at a weekly time granularity over life of mine introduces a discrete combinatorial problem space where the number of unique solution possibilities would be on the order of 10^30. It is not an exaggeration to state that for some algorithm classes, the corresponding runtime would on the order of geological time.
Many of the problem features just discussed cannot be suitably addressed by applications available within Microsoft Excel, and at least some of these issues cannot be addressed in software that uses 3rd party mathematical optimisation libraries from CPLEX or Gurobi. Our operations research experience in academia and the mining industry indicates that specific mathematical algorithms must be designed in order to efficiently, effectively, and robustly optimise this particular class of problems. A well-regarded theoretical foundation supports these conjectures on algorithm design (Wolpert and Macready, 1999; Ho and Pepyne, 2002).
When Defining the "Right Problem" Matters
Product Price Model Example
In a product planning project, complex pricing models are typically substituted with a product price that tracks an index. This might be justified by a lack of information as to how product blends will deviate from quality specifications or based on an assumption that product quality attributes will have relatively little influence on product price. Product plans created by marketing teams in this way implicitly assume price penalties from product quality will not significantly influence what products should be sold.
Figure 2 shows obfuscated results from a project where product planning first took place in BlendOpt using only an index price. This is compared to plans where optimisation involved the modelling of prices with adjustments based on quality attributes including ash, moisture, calorific value, and sulphur. While the profit implications were significant (> 4% increase in revenue, results not shown), more surprising was the extent that the product mix differed between scenarios. In particular, the results in Figure 2 and Figure 3 display greater than 50% reductions in the amount of low ash thermal coal sold (see "TH 6%" in Figure 2) and a 9.6% increase in metallurgical coal sold when product price models are accounted for during optimisation. These non-negligible financial and product differences may suggest a potential gap within the market planning exercises undertaken by some coal producers.
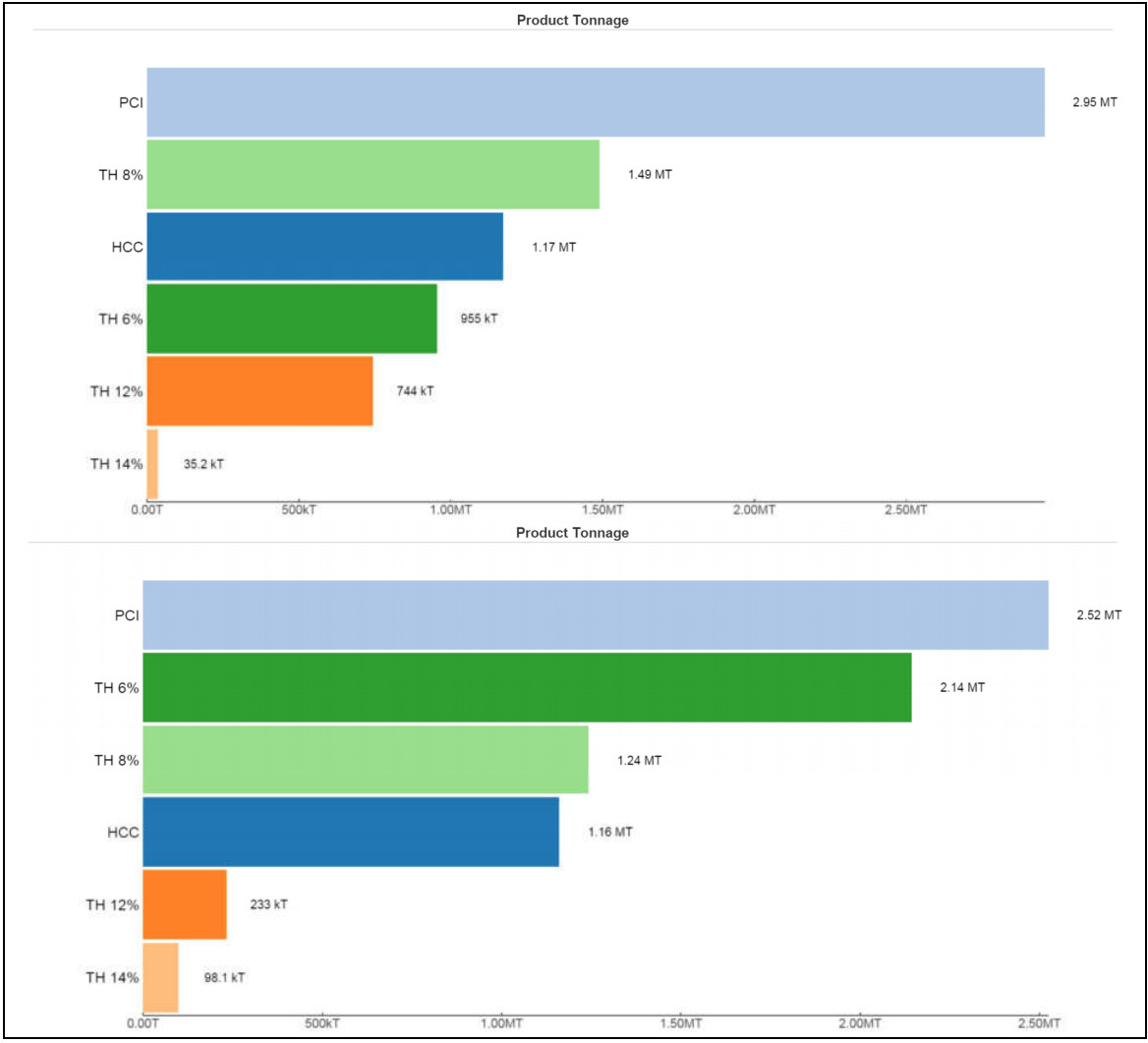
Cost Model Example
An accurate model of upstream and downstream operating costs can influence the relative financial benefits that are measured between plan alternatives. In one project, BlendOpt was configured using a cost model that accounted only for cost differences between washing and bypassing coal. BlendOpt was configured in this way because it was assumed other costs would not influence the optimality of coal processing and product planning decisions. Later, the same client configured BlendOpt with a more detailed cost model including mining, rail, port, and other costs that resulted in a total modelled cost that was comparable in magnitude to sales prices. Mathematically optimised product plans displayed substantive material differences across the two scenarios (results not shown). Optimisation with the detailed cost model resulted in plans where metallurgical coals represented over half of all coal sold. In contrast, optimisation with only a CHPP cost model indicated optimal plans would create less than 20% metallurgical coal by weight. The difference between these scenarios was surprising to the client and the origins of this unexpected result were ultimately attributed to: 1) historically unprecedented price compression within the market and 2) an unexpected modelling effect discussed below.
The chart in Figure 4 attempts to explain how costs that are upstream and downstream of the CHPP can have different consequences to plan optimality. In the illustrative example in Figure 4, two products are created from a single seam with a 20% higher processing yield associated with the thermal product. As more post-CHPP costs are added to the cost model, this has a disproportionate cost impact on products created from coal processed at higher yields. For instance, a high ash thermal coal is likely to have its total cost increase more than a coking coal as costs downstream of the CHPP increase due to the thermal coal tending to be composed of more unwashed or high yield clean coal.
The implications of this basic finding are significant: modelling an accurate balance of upstream costs (which are based on ROM tonnes) and downstream costs (which are based on product tonnes) will influence financial comparisons between plan alternatives and thereby affect the composition of a mathematically optimised plan. Plans that do not accurately account for these costs may deviate considerably from the financially optimal plan.

Challenging Pre-Existing Planning Assumptions
The ability to evaluate alternatives to long held planning assumptions can act as a catalyst for realigning decisions across a value-chain.
When planning what coal should be washed and how it should be assigned to products, it is common for intuition-based logic to be derived through an analysis of coal quality, washability and marketing team feedback. On several occasions, BlendOpt has been compared against rule-based systems that were being used to decide how coal should be processed and assigned to products. A simplistic depiction of a rule-based system is given in Figure 5.

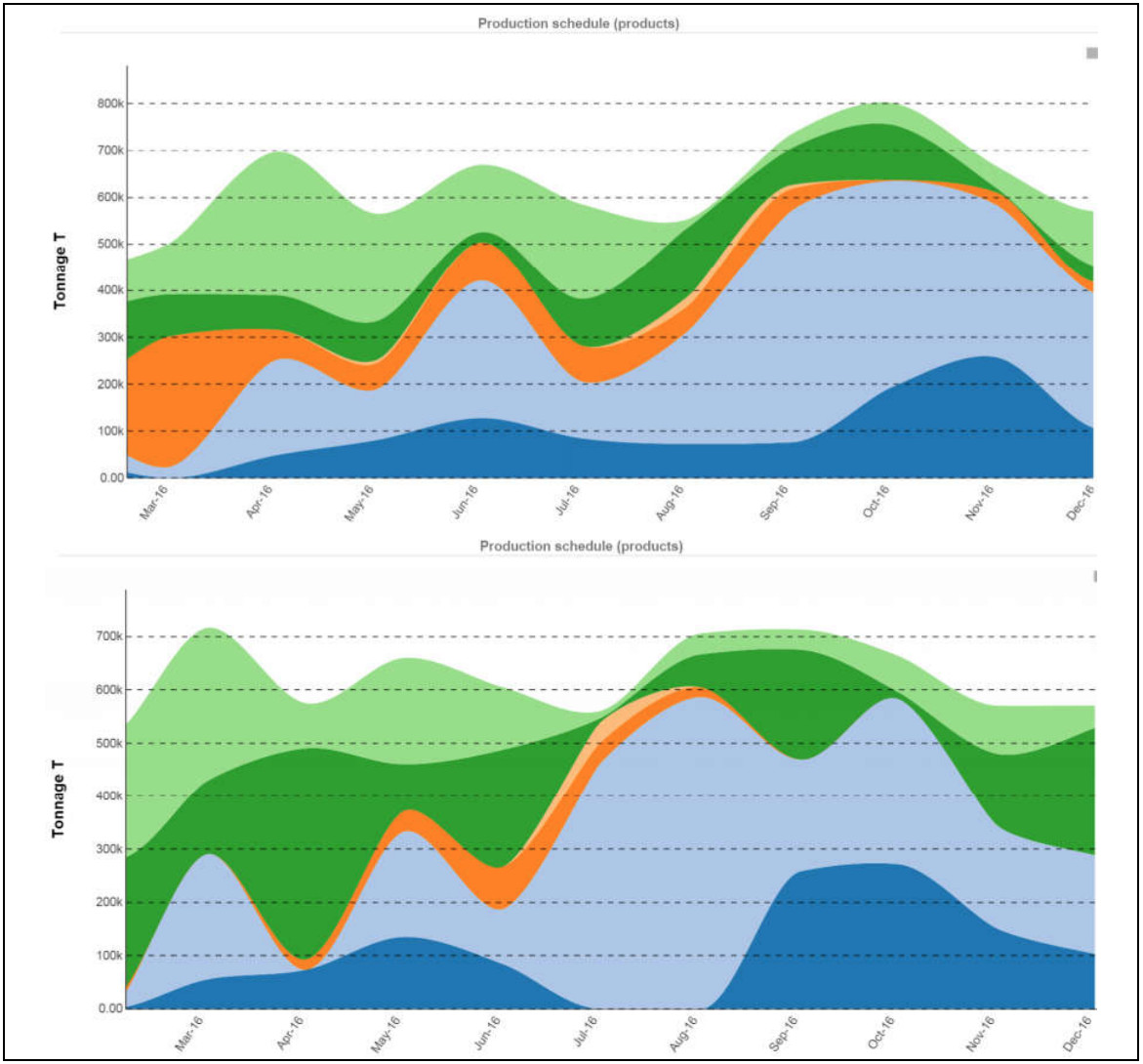
The chart on the right panel of Figure 6 displays results that were initially created using such a rule based system and were then further improved using Excel Solver. While optimisation using Excel Solver improved results significantly, the improvements did not greatly change product ratios, indicating a strong influence from the initial rule-based plan.
This can be contrasted with the results in the left panel of Figure 6 which were generated by BlendOpt. The BlendOpt plan has CHPP utilisation decreasing almost by 50% and revenue increasing by 6.8%. In comparison with the original plan, significant and frequent exceptions were made in the amount of coal that was washed (Figure 7) and in the products that were sold (Figure 6). For instance, BlendOpt sells 41% more tonnes of metallurgical coal compared with the original plan.
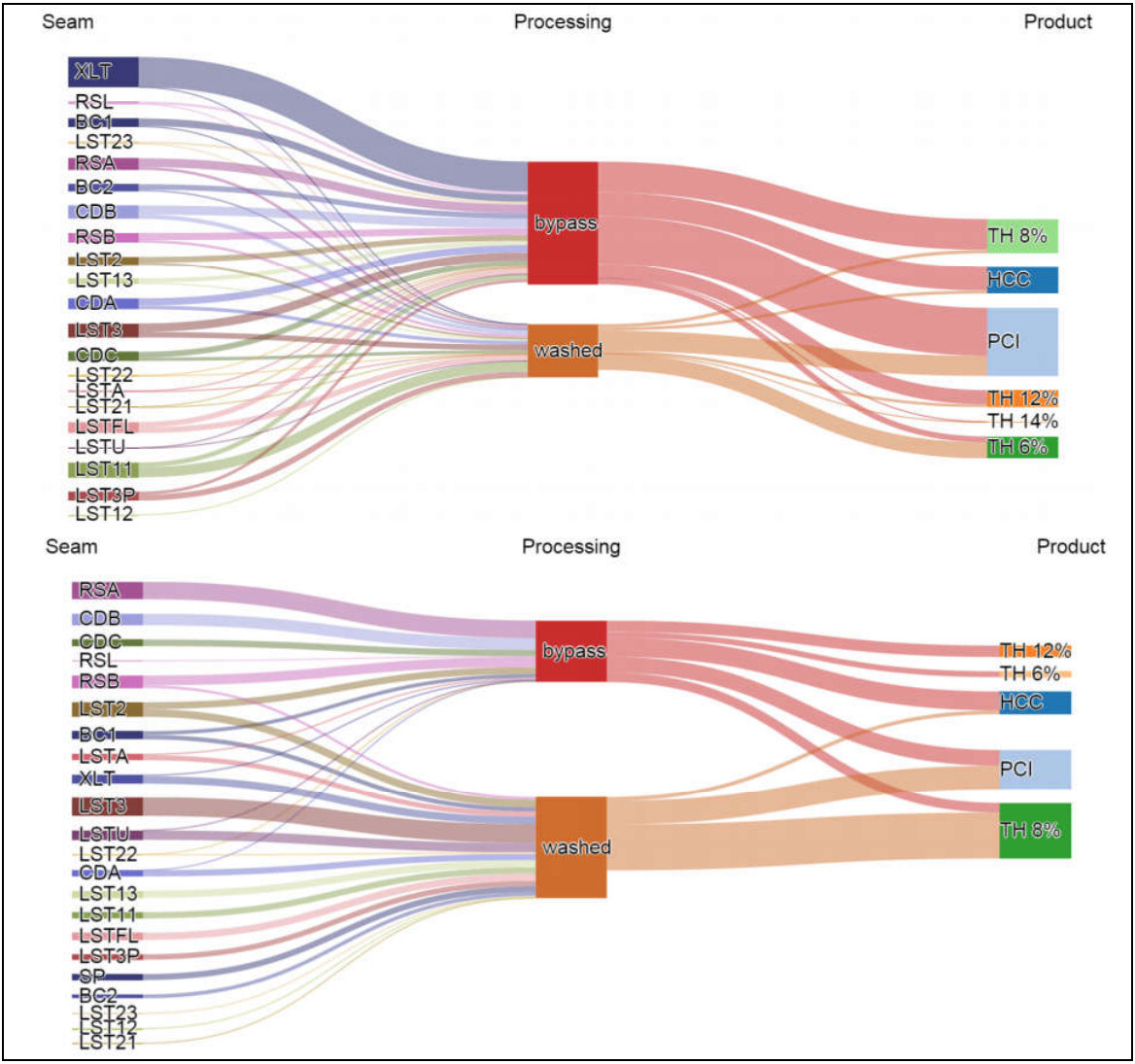
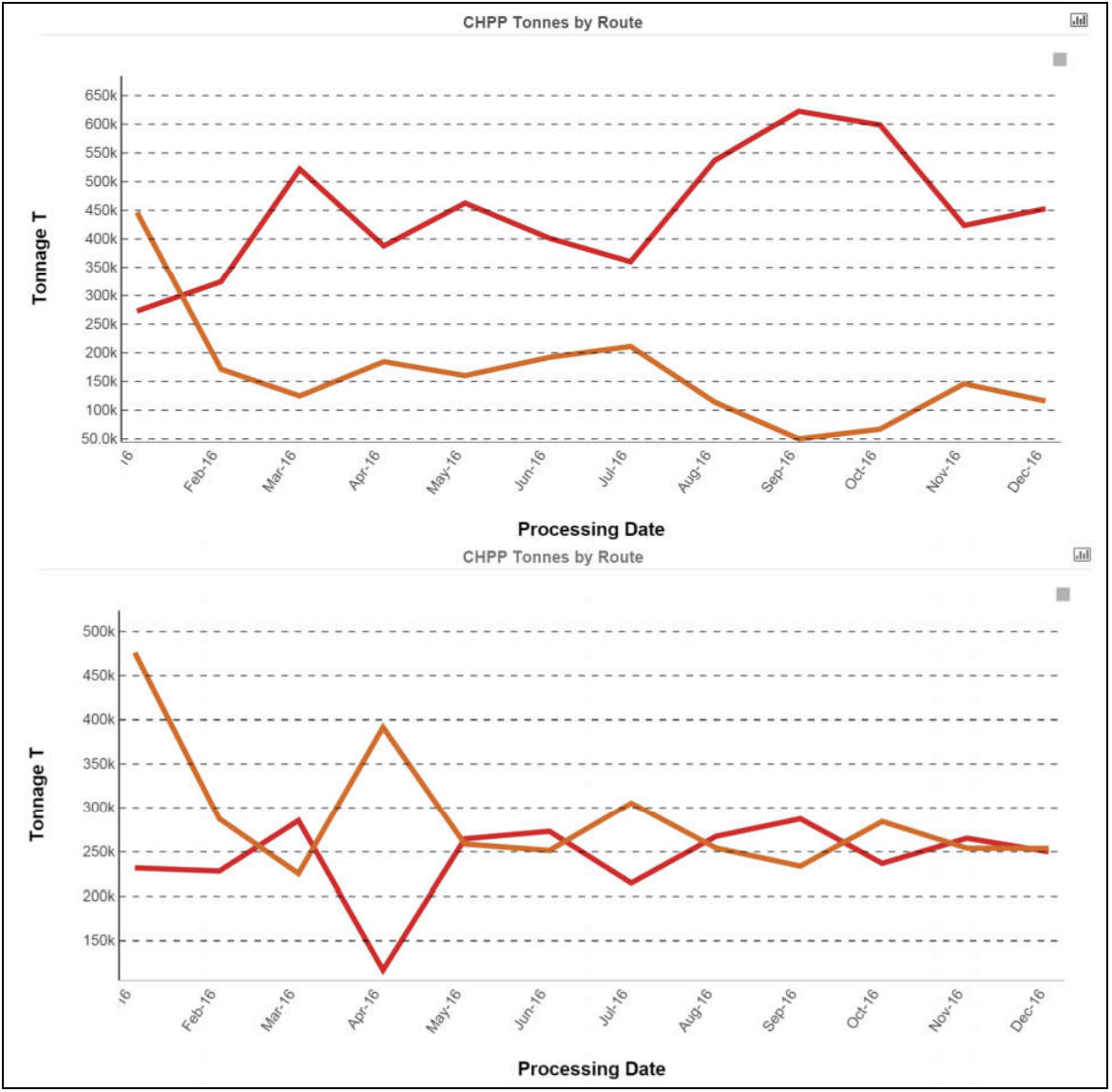
Product Planning through Decomposition
The mathematical complexity of integrated planning prevents tools such as Excel Solver from solving this class of problems in its entirely. Some coal operations utilise an educated deconstruction of the planning problem to enable optimisation tools like Excel Solver to be applied in a sequential or iterative manner.
Due to significant price differences between products, it might be assumed that maximising production of the highest price product first, and then iterating product planning from highest to lowest sale price, would correspond with an approximately optimal product plan. This is one example of how operations have sometimes used product price to deconstruct the planning process.
Following this logic, a marketing team used Excel Solver to generate a result similar to that labelled as "Heuristic" in Table 2. This planning procedure creates a large amount of P1 product; the product with the highest sale price in Table 1. Optimising the same problem in its entirety, BlendOpt generated the result shown in Table 2.
The average revenue per tonne is slightly lower in the BlendOpt plan, however BlendOpt generates significantly more total product tonnes with a plan revenue increase of approximately 5% compared to the original plan.
It is worth noting that only a relatively small amount of P1 was created in the BlendOpt result, while a substantially larger amount of the lower priced P2 was produced. It should also be noted that the scope of this project included contracted sales for P1 of 520kt, the exact amount of P1 produced by BlendOpt. Removal of the P1 contract further reduces P1 within the BlendOpt result (results not shown).
The Excel Solver plan produces lower financial results because of the lower yields that were necessary to maximize production of the highest valued low-ash thermal product. If products are optimised simultaneously, the higher revenue per tonne is more than compensated for through higher total production.


Conclusions
This article reviewed examples of non-trivial changes to calculated financial metrics from the application of BlendOpt's mathematical optimisation algorithms to the integrated coal value-chain planning problem in comparison to human intuition, Excel Solver, and rule-based techniques. Experience to date indicates that the magnitude of quantitative differences reported here are generally repeatable for multi-seam multi-product operations.
When using mathematical optimisation software, it's important the software can model those problem features that alter the mathematical relationship between decision variables and the financial objectives optimised. In this article we demonstrated examples where problem features from seemingly unrelated components of the value-chain had unexpected consequences on the financially optimal plan. For instance, price penalties were found to significantly alter the mathematically optimal product mix in one operation while a more comprehensive cost model was found to significantly alter the financially optimal plan at another operation.
Given that many planning exercises make at least some of the assumptions reviewed here, the findings presented in this article raise interesting questions regarding the magnitude of value that could be lost from current planning procedures. In today's dynamic market, easy to-use integrated planning software could become a valuable tool for competitive advantage. Some coal producers are already considering these possibilities as unprecedented pricing regimes create conditions in which historical intuition provides less meaningful guidance.
References
Ho Y.C. and Pepyne D.L. 2002, "Simple explanation of the no-free-lunch theorem and its implications", Journal of Optimization Theory and Applications, V115, N3, pp549-570.
King B. 2004, "Integrated Strategy Optimisation for Complex Operations", Orebody Modelling and Strategic Mine Planning, pp391-398.
Levinthal D.A. and March J.G. 1993, "The myopia of learning", Strategic Management Journal, V14, N8, pp95-112.
March J. G. 1991, "Exploration and exploitation in organizational learning", Organization Science, V2, N1, pp71-87.
Van Niekerk W.H. and Dippenaar R.J. 1991, "Blast-furnace coke: A coal-blending model", Journal of the South African Institute of Mining and Metallurgy, V91, N2, pp53-61.
Vasko F.J., Newhart D. D. and Strass A. D. 2005, "Coal blending models for optimum coke making and blast furnace operation", Journal of the Operational Research Society, V56, pp235-243.
Whittle G. 2010, "Enterprise Optimisation", Mine Planning and Equipment Selection (MPES) Conference, pp105-117.
Wolpert D. H. and Macready W. G. 1997, "No free lunch theorems for optimization", IEEE Transactions on Evolutionary Computation, V1, N1, pp67-82.
Would you like to know more?
Do you optimize product placement into the market?
Do you know when Demurrage adds value (can you spot “value justified” demurrage)?
Do you know in what situations your stockpile quality models increase contract rejection risk?
Does your planning software require stable operations, predictable markets, consistent orebodies?
Can you run scenarios to understand your options?
Does your tactical scheduling software automatically synchronize with your longer term planning tools?
Do your schedules reflect conditions on the ground?
Are your schedules tossed in the bin on day 1?